 Bilangan adalah suatu konsep dalam ilmu matematika yang digunakan untuk pencacahan dan pengukuran.
Bilangan adalah suatu konsep dalam ilmu matematika yang digunakan untuk pencacahan dan pengukuran.Di dalam matematika, bilangan dikelompokkan ke dalam beberapa jenis bilangan yang tersusun secara hirarki. Pengelompokan jenis-jenis bilangan tersebut disebut sebagai struktur bilangan.
Pemahaman Struktur Bilangan
Pemahaman mengenai struktur bilangan sangat diperlukan dalam memahami beberapa materi pelajaran matematika yang lain, seperti himpunan, relasi dan fungsi, persamaan dan pertidaksamaan linier, dan beberapa materi yang lainnya.Berikut akan dijelaskan mengenai bagian-bagian dari struktur bilangan seperti yang ditunjukkan oleh gamber di bawah ini.
Bilangan Kompleks
Bilangan kompleks adalah bilangan yang terdiri atas gabungan bilangan real dan bilangan imajiner. Oleh karena itu, bilangan kompleks (𝒛) dapat dinotasikan dengan hubungan penjumlahan 𝒛 = 𝑎 + 𝑏𝑖, dimana 𝑎, 𝑏 ∈ 𝑅 (𝑎 dan 𝑏 anggota bilangan real), dengan 𝑎 merupakan bagian real dan 𝑏𝑖 merupakan bagian imajiner.
Contoh: 2 + 5𝑖, 7 ₋ 3𝑖
Contoh: ⅗, 0,56, log 2
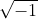 .
.
Contoh: 2 + 5𝑖, 7 ₋ 3𝑖
Bilangan Real
Bilangan real adalah bilangan yang dapat disajikan dalam bentuk desimal tak terbatas. Sehingga bilangan real mencakup bilangan rasional dan bilangan irasional.Contoh: ⅗, 0,56, log 2
Bilangan Imajiner
Bilangan imajiner merupakan suatu bilangan yang tidak nyata, dalam artian bahwa bilangan tersebut bukan merupakan bilangan rasional maupun bilangan irasional. Bilangan imajiner dilambangkan sebagai 𝑖 yang memiliki sifat 𝑖²=-1, dimana 𝑖 ∈ 𝑅 (𝑖 anggota bilangan real). Dengan demikian dapat dikatakan bahwa bilangan imajiner 𝑖 sama nilainya denganContoh: 3𝑖, -9𝑖,
Bilangan Rasional
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan 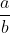 , dimana 𝑎 dan 𝑏 adalah anggota bilangan bulat, dan 𝑏 tidak sama dengan 0.
, dimana 𝑎 dan 𝑏 adalah anggota bilangan bulat, dan 𝑏 tidak sama dengan 0.
Contoh: ⅔, ⅙, 0,25 (sama nilainya dengan ¼), 2 (sama nilainya dengan Bilangan Irasional
Bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk pecahan. Jika bilangan irasional ditulis dalam bentuk desimal, maka bilangan itu tidak mempunyai pola yang berulang secara teratur.Contoh: 0,12012200...,
Bilangan Pecahan
Bilangan pecahan adalah bilangan yang dapat dinyatakan dalam bentuk pecahan 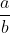 , dimana 𝑎 dan 𝑏 adalah anggota bilangan bulat, dan 𝑏 tidak sama dengan 0 dan atau 1. Bilangan pecahan merupakan bagian dari bilangan rasional, tetapi bilangan rasional belum tentu adalah bilangan pecahan (3 adalah bilangan pecahan karena nilainya sama dengan
, dimana 𝑎 dan 𝑏 adalah anggota bilangan bulat, dan 𝑏 tidak sama dengan 0 dan atau 1. Bilangan pecahan merupakan bagian dari bilangan rasional, tetapi bilangan rasional belum tentu adalah bilangan pecahan (3 adalah bilangan pecahan karena nilainya sama dengan  , tetapi bukan merupakan bilangan pecahan)
, tetapi bukan merupakan bilangan pecahan)
Contoh: ⅖, ⅚, 0,625 (sama nilainya dengan ⅝)
Contoh: -2, 0, 3, 17
Contoh: 0, 3, 18, 27
Contoh: -15, -8, -1
Contoh: 1, 6, 87
Contoh: 2, 36, 98
Contoh: 11, 75, 109
Contoh: 17, 41, 83
Contoh: 21, 49, 77
Contoh: ⅖, ⅚, 0,625 (sama nilainya dengan ⅝)
Bilangan Bulat
Bilangan bulat adalah semua bilangan yang bukan merupakan bilangan pecahan. Bilangan bulat terdiri dari gabubungan antara bilangan nol, bilangan asli, dan bilangan negatifnya.Contoh: -2, 0, 3, 17
Bilangan Cacah
Bilangan cacah adalah gabungan antara bilangan asli (bilangan bulat positif) dan bilangan nol.Contoh: 0, 3, 18, 27
Bilangan Bulat Negatif
Bilangan bulat negatif adalah bilangan bulat yang memiliki tanda negatif (-) sebelum angkanya.Contoh: -15, -8, -1
Bilangan Asli
Bilangan asli adalah bilangan yang digunakan untuk membilang (menghitung satu satu). sehingga bilangan asli merupakan bilangan bulat yang dimulai dari bilangan 1.Contoh: 1, 6, 87
Bilangan Genap
Bilangan genap adalah bilangan bulat yang selalu habis jika dibagi dengan bilangan 2.Contoh: 2, 36, 98
Bilangan Ganjil
Bilangan ganjil adalah bilangan bulat yang tidak habis jika dibagi dengan 2.Contoh: 11, 75, 109
Bilangan Prima
Bilangan prima adalah bilangan bulat lebih dari satu dan hanya bisa dibagi habis oleh bilangan 1 dan bilangan itu sendiri.Contoh: 17, 41, 83
Bilangan Komposit
Bilangan komposit adalah bilangan bulat lebih dari satu yang bukan merupakan bilangan prima.Contoh: 21, 49, 77


0 Response to "Struktur Bilangan"
Posting Komentar